You are here: start » whitepapers » sequences » emsequence
Ring Sequence: Chopping and Adding
Students who are just beginning upper-division courses are being asked to simultaneously learn physics concepts, use mathematical processes in new ways, apply geometric reasoning, and use extended multi-step problem solving. Having students successfully deal with a problem such as finding the magnetic field in all space due to a spinning ring of charge is a significant challenge. If we are to avoid doing the thinking for them and creating a template they can use, then we must create a sequence of learning opportunities that allow them to genuinely develop for themselves the ability to solve a problem like this.
We created a sequence of five small group activities that help students do deeper thinking while making each of the steps manageable. These five activities take roughly 30 to 60 minutes each and are designed to be used over the course of one or two months in conjunction with other forms of instruction such as lecture, individual homework, computer visualizations, and kinesthetic activities. Additionally, we have included two lectures to help students reason geometrically about charge distributions and electric potentials.
A more in-depth discussion of the rationale, student thinking, and the way these activities fit together can be found in a discussion of how these activities break the learning into manageable pieces
Lecture: Electric Potential
Students may be familiar with the iconic equation for the electric potential (due to a point charge): $$\text{Iconic:} \qquad V=\frac{1}{4 \pi \epsilon_0} \frac{Q}{r}$$ With information about the type of source distribution, one can write or select the appropriate coordinate independent equation for $V$. For example, if the source is a linear (i.e. 1 dimensional): $$\text{Coordinate Independent:} \qquad V=\frac{1}{4 \pi \epsilon_0} \int\frac{\lambda | d\vec r' |}{| \vec r - \vec r' |}$$ Looking at symmetries of the source, one can choose a coordinate system and write the equation for the potential in terms of this coordinate system. Note that this step is often combined with the following step, though one may wish to keep them separate for the sake of careful instruction. $$\text{Coordinate Dependent:} \qquad V=\frac{1}{4 \pi \epsilon_0} \int\frac{\lambda |ds'\ \hat s + s'\ d\phi'\ \hat \phi + dz'\ \hat z|}{| s'^2 + s^2 +2ss' \cos(\phi-\phi') + z^2|}$$ Using what you one about the geometry of the source, one can simplify the expression. For example, if the source is a ring of charge with radius $R$ and charge $Q$ in the $x$-, $y$-plane the integral becomes: $$\text{Coordinate and Geometry Dependent:} \qquad V=\frac{1}{4 \pi \epsilon_0}\, \frac{Q}{2\pi R} \int_0^{2\pi}\frac{R\ d\phi'}{| R^2 + s^2 +2Rs \cos(\phi-\phi') + z^2|}$$
Lecture: Chop, Calculate, and Add
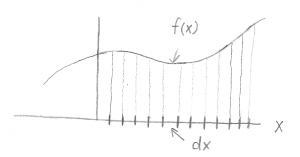
- To find the area under a curve, one may chop up the x-axis into small pieces (of width $dx$). The area under the curve is then found by calculating the area for each region of $dx$ (which is $f(x) dx$) and then summing up all of those areas. In the limit where $dx$ is small enough, the sum becomes an integral.
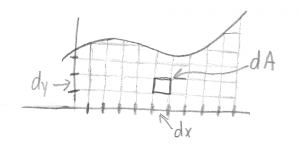
- One could also find the area under a curve by chopping up both the x- and y-axes (chop), calculating the area of each small area under the curve (calculate), and adding all of those together with a double sum or double integral.
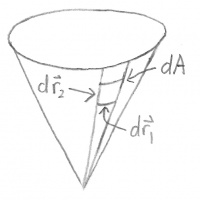
- This approach can be used to find the area of a cone, where the 'horizontal' length of each area is $r d\phi$ and the 'vertical' length is $dr$, giving an area of $dA = r d\phi dr$. It is important to make sure that the limits of integration are appropriate so that the integrals range over the whole area of interest.
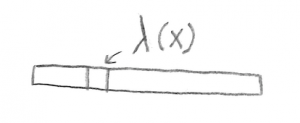
- If one wants to calculate something other than length, area, or volume, such as if one sprinkled charge over a thin bar, then chop, calculate, and add still works. Again, chop the bar up into small lengths of $dx$. Then calculate the charge $dQ$ on each length ($dQ = \lambda dx$), and add all of the $dQ$s together in a sum or integral.
- This also works for calculating something (such as charge) over a volume. For a thick cylindrical shell with a charge density $\rho(\vec r)$, chop the shell into small volumes of $d \tau$ (which will be a product of 3 small lengths, e.g. $d \tau = r d\phi\ dr\ dz$), multiply this volume by the charge density at each part of the shell (defined by e.g. $r, \phi,$ and $z$), and add the resulting $dQ$s together.
Activities: Electrostatics
- Electrostatic Potential Due to Two Point Charges (Estimated time: 50 minutes, Wrap-Up: 30 minutes): This activity is also part of the Power Series Sequence. Students use what they learned from The Distance Between Two Points - Star Trek and apply what they know about power series approximations to find a general expression and asymptotic solution to the electrostatic potential due to two point charges. Though the charge distribution students consider is elementary, the ideas and techniques used are applied later on to the more difficult ring of charge.
- Electrostatic Potential Due to a Ring of Charge (Estimated time: 40 minutes, Wrap-Up: 10 minutes): Many students coming into their junior year have likely seen the electrostatic potential due to a ring of charge with high symmetry. In this small group activity, students aim to generalize the expression for the potential by applying what they have learned about charge densities, power series approximations, and various geometries. In order to accomplish this, students practice breaking the problem up into “manageable” pieces: finding a relationship for the charge density, understanding the geometry of the problem, setting up the correct integral, and then using power series approximations to evaluate the potential in some given region. Solving this problem is a big step for many students and also prepares them for the more difficult problem of finding the electric field due to a ring of charge.
- Electric Field Due to a Ring of Charge (Estimated time: 40 minutes, Wrap-Up: 10 minutes): Now that students have had experience calculating the electrostatic potential due to a ring of charge, another layer of complexity is added to the problem. In this small group activity, students use the definition of the electric field as $\vec{E}(\vec{r})=\frac{1}{4\pi\epsilon_0}\int_{ring}{\frac{\lambda(\vec{r'})(\vec{r}-\vec{r'})|d\vec{r'}|}{|\vec{r}-\vec{r'}|^3}} $ in order to work out the electric field due to a ring of charge. Again, students must break this problem into multiple steps, making the problem as a whole more manageable. This allows students to develop a template for solving similar problems. Moreover, this activity exemplifies the approach the Paradigms uses of “potential first”. Using techniques from the previous activity on the electrostatic potential, students tend to have an easier time transitioning from scalar fields to vector fields.
Activities: Magnetostatics
- Magnetic Vector Potential Due to a Spinning Ring of Charge (Estimated time: 40 minutes, Wrap-Up: 10 minutes): In many ways, this small group activity is simply the magnetic analogy to Electrostatic Potential Due to a Ring of Charge. By this time students are likely to recognize the problem is headed toward an integral which they will be approximated using power series. However, the set up for this problem is more complex because students now must think about current densities and the inherent vector nature of the magnetic vector potential. Again, in order to solve this problem, students practice breaking the problem into multiple steps, allowing them to develop a template approach for solving such problems.
- Magnetic Field Due to a Spinning Ring of Charge (Estimate time: 40 minutes, Wrap-Up: 10 minutes): Building from their experience with the previous exercises, by this small group activity many students have an idea on how to solve this problem. Using the techniques they learned and the template they have constructed from the four previous activities, students obtain an expression for the magnetic field due to a spinning ring of charge, a feat for any junior-level physics major.
A Master's Project Paper describing the sequence of the five E&M activities: