You are here: start » courses » lecture » pplec » pplecapproxbe1d
Approximating the Internal Energy for a 1-Dimensional Chain (30 minutes)
Note: Time permitting, this lecture would also work well as an activity for students to tackle in small groups.
- Present the students with the following prompt:
A 1-dimensional chain contains N atoms and has total length L. Find the total energy stored in the lattice when:
a) $T > \frac{\hbar \omega_{max}}{k_{B}}$
b) $T < \frac{\hbar \omega_{max}}{k_{B}}$
- Solutions
a) Since the temperature is above the “freeze out” zone, the energy stored in the lattice can be estimated using the equipartition theorem.
$$U_{tot}=\left(\text{Total # modes}\right)\left(k_{B}T\right)=Nk_{B}T \; \; . $$
b) For this limiting case, we still want to find the number of modes and multiply by $k_{B}T$. However, the higher modes at this temperature are now “frozen out”. Our strategy will be to find the number of modes that have not been frozen out for a given temperature.
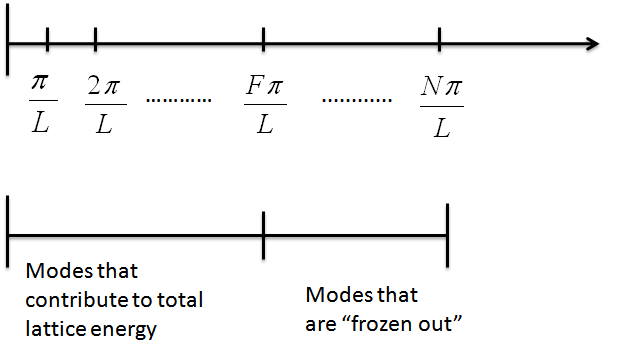
- First, we must find what the highest-allowed wave vector is. Recall that the possible wave vectors for all the normal mode wave functions are:
$$\frac{\pi}{L}, \frac{2\pi}{L}, \frac{3\pi}{L},…,\frac{F\pi}{L},…, \frac{N\pi}{L}$$
where the highest-allowed wave vector $k_{freeze}=\frac{F\pi}{L}$.
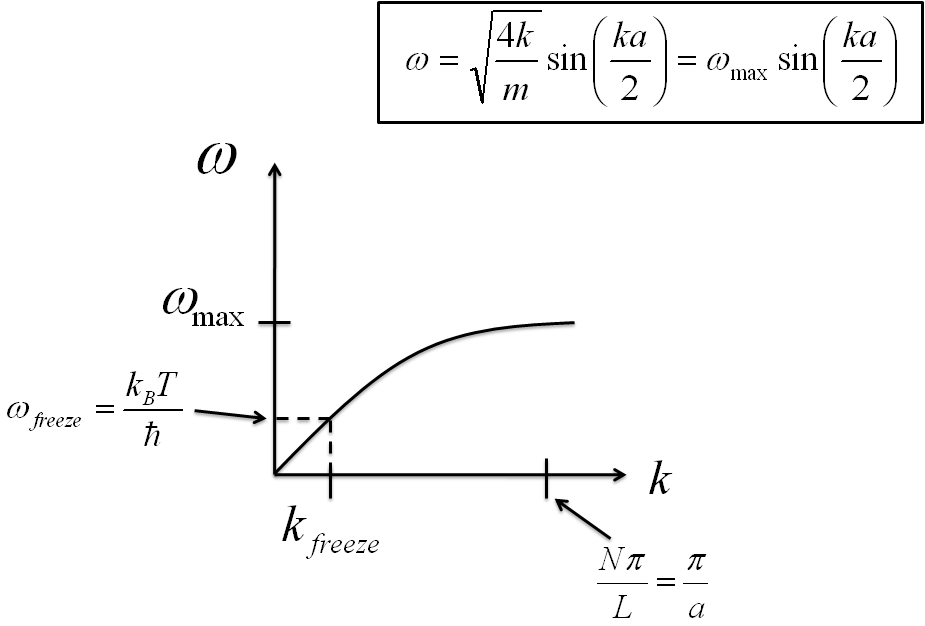
We can also plot each of these wave vectors on the dispersion relation for the N-chain oscillator as seen below.
- Let's see what we can find out about k_{freeze} from the dispersion relation. Recall that the dispersion relation for a 1-dimensional chain is
$$\omega(k)=\omega_{max}\sin{\frac{ka}{2}} \; \; ,$$
where $\omega_{max}=\sqrt{\frac{4\kappa}{m}}$. If we approximate that $k_{freeze}$ is a small value (a reasonable approximation for our limiting temperature condition), then we can insert $\omega_{freeze}$ and $k_{freeze}$ into the dispersion relation and simplify to
$$\omega_{freeze} \approx \omega_{max}\frac{k_{freeze}{a}}{2} \; \; . $$
- We still have two unknowns, so we need another equation to help us. Ask the class if they can think of how we can find more information about $\omega_{freeze}$. If they struggle, remind them that the allowed frequencies and wave numbers for normal modes are quantized; what else is quantized? The energy stored in every normal mode of a crystal is equal to
$$U_{mode}=\left(n_{phonon}+\frac{1}{2}\right)\hbar \omega_{mode}=k_{B}T \; \; .$$
Since we are in the freeze-out zone, we assume that our phonon number is at it's lowest nonzero value of $n_{phonon}=\frac{1}{2}$; the frequency of the highest node that does not freeze out must be
$$\omega_{freeze}=\frac{k_{B}T}{\hbar} \; \; . $$
- We now have two equations with two unknowns $\omega_{freeze}$ and $k_{freeze}$. Setting the equations
$$\omega_{freeze}=\frac{k_{B}T}{\hbar} \; \; \; \; \; \; \; \text{and} \; \; \; \; \; \; \; \omega_{freeze} = \omega_{max}\frac{k_{freeze}{a}}{2}$$
equal to each other will give us that the freeze-out wave vector is
$$k_{freeze}=\frac{2k_{B}T}{a\hbar \omega_{max}} \; \; .$$
- Now that we have $k_{freeze}$, we can find the number of modes that are not frozen out. This is done as so:
$$\text{# modes not frozen out}=\frac{\text{highest wave vector}}{\text{spacing between each wave vector}} \; \; .$$
In our case, this looks like:
$$\text{# modes}=F=\frac{k_{freeze}}{\frac{\pi}{L}} \; \; ,$$
$$F=\frac{2Lk_{B}T}{\pi a \hbar \omega_{max}}=\frac{2Nk_{B}T}{\pi \hbar \omega_{max}} \; \; .$$
- Finally, the number of modes can be used to calculate the total energy of the lattice:
$$U_{tot}=\left(\frac{2Nk_{B}T}{\pi \hbar \omega_{max}}\right)\left(k_{B}T\right) \; \; .$$
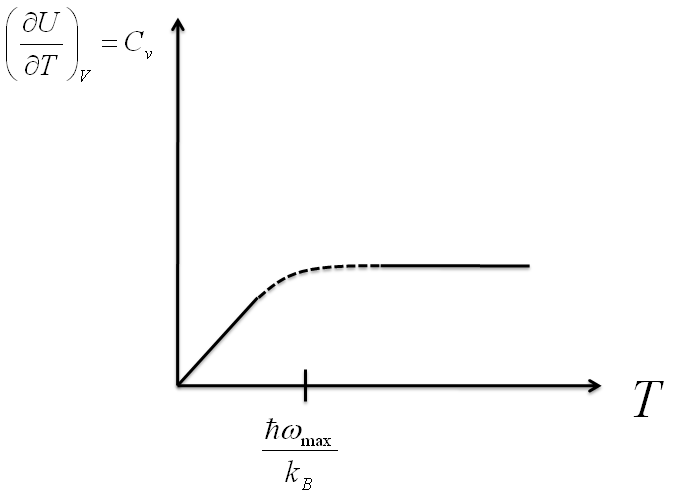
- With the equations derived from each exercise, we could create graphs that approximate both the total energy of the 1-D chain and the heat capacity of the chain at the limits each solution is constrained to.
Notice that when $T < \frac{\hbar \omega_{max}}{k_{B}}$,
$$C_{v} \propto T \; \; . $$
What can we do about the range where $T=\frac{\hbar \omega_{max}}{k_{B}}$ ?