- §1. Practice
- §2. The Getaway
- §3. Angles are not Invariant
- §4. Interstellar Travel
- §5. Cosmic Rays
- §6. The Doppler Effect
Cosmic Rays
Consider muons produced by the collision of cosmic rays with gas nuclei in the atmosphere 60 kilometers above the surface of the earth, which then move vertically downward at nearly the speed of light. The half-life before muons decay into other particles is 1.5 microseconds ($1.5\times10^{-6}$ s).
- Assuming it doesn't decay, how long would it take a muon to reach the surface of the earth?
- Assuming there were no time dilation, approximately what fraction of the muons would reach the earth without decaying?
- In actual fact, roughly $1\over8$ of the muons would reach the earth! How fast are they going?
1. Without much loss of accuracy, assume the muons travel at the speed of light. Then it takes them \begin{equation} {60 \hbox{km}\over3\times10^8 {\hbox{m}\over\hbox{s}}} = 200 \mu\hbox{s} \end{equation}
2. $\displaystyle 200 \mu\hbox{s}$ is $\displaystyle{200\over1.5}={400\over3}$ half-lives, so only $2^{-{\scriptstyle400\over\scriptstyle3}}$ of the muons reach the earth!
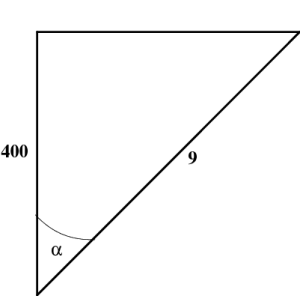
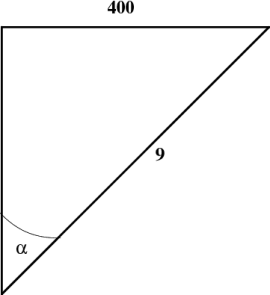
Figure 7.11: Hyperbolic triangles for the cosmic ray example.
3. First solution: This corresponds to 3 half-lives. Thus, the time is dilated by a factor of ${{400/3}\over3}$, so that \begin{equation} \cosh\alpha = {400\over9} \end{equation} But \begin{equation} {v\over c} = \tanh\alpha = {\sqrt{400^2-9^2}\over400} \approx .99974684 \end{equation} See the first drawing in Figure 7.11.
Second solution: The above argument assumes $v\approx c$! (This was used to obtain the figure 200 $\mu$s in part (a), which is hence only an approximation.)
A more accurate argument would use the fact that the muons travel 60 km in $4.5\times10^{-6}$ s (of proper time). Thus, \begin{equation} \sinh\alpha = {(60 \hbox{km})(1000 {\hbox{m}\over\hbox{km}})\over (4.5\times10^{-6} \hbox{s})(3\times10^8 {\hbox{m}\over\hbox{s}})} = {400\over9} \end{equation} so that \begin{equation} {v\over c} = \tanh\alpha = {400\over\sqrt{400^2+9^2}} \approx .99974697 \end{equation} See the second drawing in Figure 7.11.
It is important to realize not only that the second answer is more accurate than the first (assuming sufficient accuracy in the original data!), but also that that the “shortcut” used in the first answer is justified! 1)