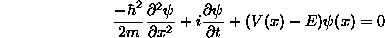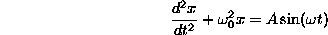Differential Equations

To classify differential equations we use a variety of terms, the most usual ones being,

ordinary - partial

A differential equation is called ordinary if the unknown function and its derivatives depend only on one independent variable. In a partial differential equation the unknown function and its derivatives depend on at least two independent variables.
Example:
The time-dependent Schrödinger equation,

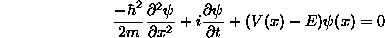
is a partial differential equation as it contains two independent variables x and t.

order

The order of a linear equation is determined by the order of the highest derivative in the equation.
Example:
The equation describing the harmonic oscillator,

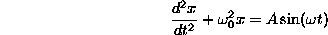
is a second-order differential equation as the the highest derivative is of second order. Sometimes it is possible to solve a differential equation by reducing it to one of lesser order. However, this does not change the order of the initial equation.

homogenous - inhomogenous

A differential equation is called homogenous if every term in it depends on the unknown function or its derivatives. It is inhomogenous if there is at least one term which depends only on the independent variables or is a constant different than zero.
Example:
The differential equation of a driven harmonic oscillator,

is inhomogenous as the term on the right only depends on t.

linear - nonlinear

A linear differential equation contains only linear terms of the unknown function and its derivatives.
Example:
The differential equation describing a realistic pendulum,

is a common example.

degree

If a nonlinear differential equation can be expressed as a polynomial of the unknownfunction and its derivatives, then the degree of this differential equation is the highest power of this polynomial.