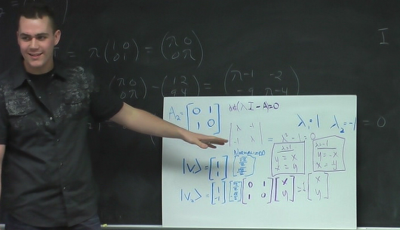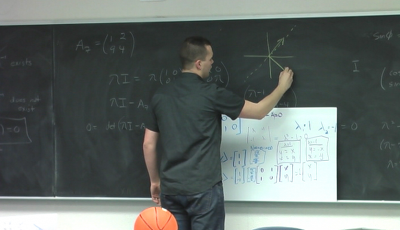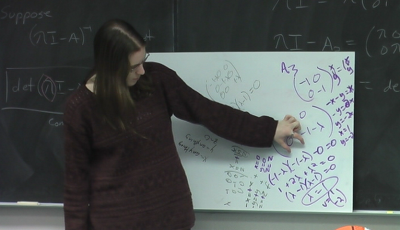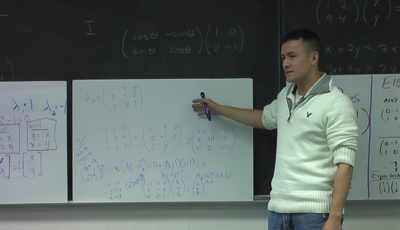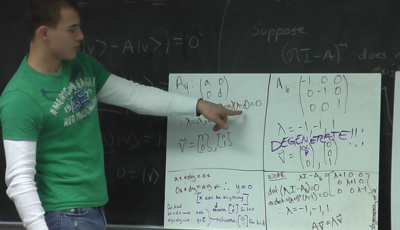You are here: start » whitepapers » narratives » eigenvectorslong
Example Wrap-up Discussion #2
Physics Paradigms Preface
Thursday, January 10, 2008 (2nd hour, Day 4)
This class session provides a second example of a “wrap-up” discussion in which junior-level physics students and their instructor ‘made sense’ together of the thinking the students had been doing in small groups. The goal of this ‘compare and contrast’ wrap-up discussion was to help the students envision connections among geometric and algebraic representations of the mathematics they would be using during the coming weeks of instruction in quantum mechanics.
This wrap-up discussion occurred on Thursday, January 10, 2008, the fourth day of a week of instruction known as the “Preface.” The instructor, Corinne Manogue, had designed the content and activities for the Preface as follows:
- Day 1 had been a 50-minute interactive lecture that introduced basic matrix manipulations such as matrix multiplication and determinants.
- Day 2 had been a double period. First the students worked in small groups. Each group used a given matrix to transform a set of given vectors and then plotted the transformed vectors graphically. The set of given vectors had included eigenvectors, those whose direction would not be changed by being operated upon by one of the matrices. During the wrap-up discussion, the students had considered similarities and differences in how the various matrices had transformed the same given vectors in various ways (SEE Instructor's Guide for Linear Transformations Activity and Narrative for Linear Transformations Activity). Corinne had designed Day 2’s problems to develop the idea that an eigenvector is an arrow in space whose direction is not changed by a transformation.
- Day 3 had been a 50-minute interactive lecture that presented properties of rotation matrices in two and three dimensions.
- Day 4 was another double period. Its focus was a set of linear algebra problems that Corinne had designed to illustrate nuances in solving for the eigenvalues and eigenvectors of particular matrices. She had demonstrated a straightforward example in a brief lecture and then had used a small group activity to give the students experience with exceptional cases that were trickier. The six small groups had worked on different problems and were presenting their solutions to the whole group during the wrap-up discussion.
- Day 5 would complete the Preface with a 50-minute interactive lecture that presented the abstract properties of vector spaces and linear transformations.
The goals of Day 4’s small group activity and wrap-up discussion were for the students to learn an algebraic procedure for finding eigenvalues and eigenvectors for a matrix and to see that the vectors that they were getting from their algebraic calculations were the same ones that they had seen to be unchanged when plotted graphically on Day 2. (See the Instructor's Guide for the Eigenvectors and Eigenvalues activity.) By comparing and contrasting the solutions presented during the wrap-discussion, the students could gain a deeper understanding of the relations between geometric and algebraic representations of eigenvectors. During their study of quantum mechanics in the weeks ahead, Corinne wanted the students to understand that finding eigenfunctions for the Hamiltonian would mean looking for the functions that are unchanged or just scaled by a constant.
The six small groups of students had worked on large whiteboards at their tables as shown in Figure 1.
By working together in this way, the students were learning to speak the specialized language that physicists use in thinking about quantum phenomena. Corinne and her teaching assistant had looked over the writing and sketches on the white boards as they moved from group to group and listened in to what the students were saying. As they perceived the need or were questioned, they engaged the small groups in conversation about what the students were doing and thinking.
The following interpretative narrative presents what happened during the January 10, 2008 wrap-up discussion of the set of eigenvalue/eigenvector problems shown in the Appendix. The purpose of the narrative is to provide an example of a wrap-up discussion with commentary about ways in which the instructor was choosing to guide this process.
In developing this interpretative narrative, Corinne and her colleagues viewed a video of the class session and discussed aspects that seemed of interest. They recorded some of their reflections as they spoke together and some as they viewed the video individually at other times. Emily van Zee then used these reflections to craft the first draft of the narrative in a form that draws on her research in the tradition of ethnography of communication (Hymes, 1972; Philipsen & Coutu, 2004; van Zee & Minstrell, 1997a,b), a discipline that studies cultures through the language phenomena observed. This interpretative narrative presents an example of an instructor engaging students as novice participants in the culture of “thinking like a physicist.”
Initiating the Wrap-up Discussion [00:22:43.19]- [00:23:00.17]
When Corinne called the small groups together for the wrap-up discussion, she was quite explicit in stating her intentions, that she had demonstrated an easy generic case for them and then had engaged the small groups in cases “that have something special about them…that you need to notice.” All of the examples that the students had been working on in their small groups were ones that had either stumped her or her students in the past. Her intent in the wrap-up discussion was to bring out the small number but frequently encountered ways of being stumped in solving for a matrix’s eigenvalues and eigenvectors.
In acknowledging the challenge of the work the students had been doing, Corinne also affirmed their image of themselves as future physicists, “if you're going to have problems, I wanted you to have them here in class and not two years from now when you're trying to solve one of these by yourself in a job somewhere.” Then she issued a direct order “So I want you to pay attention to the presentations, particularly today, pay attention to the presentations of all of the groups because all of these have some funny little nuance to them.”
As shown in Figure 2, each group’s presenter placed the group’s white board on the ledge of the blackboard in the front of the room so that all could see their work. The other students remained in small groups at their tables. Corinne sat at a table near the back of the room. By placing herself within the class, she ensured that in talking to her, the presenter also would be addressing the entire class. From this position, she also could engage the entire class in conversation as needed.
Calculating and Representing Complex Eigenvalues and Eigenvectors: Group 1 [00:23:00.17] - [00:30:23.28]
The first group to present had produced the solution shown in Figure 3 [00:24:27.26] for the two dimensional matrix $A_1$. The group’s presenter began by identifying the matrix they had been given, “So this is, $A$ one is our matrix: zero, minus one, one, zero.”
Corinne interrupted to make a connection to the problems they had worked on earlier in the week, “Before you go on, this is one of the one's from Tuesday's activity; what group had this transformation?” She wanted the students to think back to what they had done in the previous activity in order to bring the resources that they had developed there to this discussion. By making such connections explicit, she was modeling ways of thinking that she wanted the students to adopt, seeking prior knowledge that can be brought to bear on the current focus of attention.
After a group finally acknowledged working with this matrix during Tuesday’s activity, Corinne asked, “What was [the transformation]?” and pressed for details, “Rotation? What kind of rotation?” After a student responded “ninety degrees,” she supplied her preferred language, “Pi over two” which prompted some grins and chuckles from students amused by what was becoming a class in-joke, her insistence on shifting to using radians rather than degrees in describing angles. She was insisting on this because using radians is a professional habit she wanted them to form. They would be doing many power series expansions in the weeks ahead and using radians rather than degrees would be necessary to get correct answers.
“Which way?” Corinne asked as she continued to probe for specifics about the rotation. One of the students commented, “We didn't have that one, we had negative one on that one,” pointing downward to indicate they had worked with the matrix $$\pmatrix{0& 1\cr –1& 0}$$ rather than $$\pmatrix{0& –1\cr 1& 0}$$ to which she responded, “ You had the other one, you had the inverse” thereby giving a name for what the student was thinking. She had briefly introduced inverse transformations in a previous class and was spontaneously taking advantage of something that came up in this class discussion to reinforce the new concept.
After reviewing the magnitude and direction of the rotation, she asked, “Okay, and what vectors were unchanged by that transformation?” After a student responded, “None,” she summarized the result she wanted them to remember, “None. Because this is a rotation. So we're looking for the vectors that were unchanged, right? And there were none.”
She also explicitly asked a meta-cognitive question to alert the students to how they should be thinking as they listened to the upcoming presentations, “You're all aware now of what the situation is?” By reviewing that none of the given vectors tried on Tuesday were unchanged when transformed by this matrix, she had set the stage for the coming class discussion that would resolve the issue: are there any eigenvectors for rotations?
The presenter for this first group then articulated his group’s method for finding the eigenvalues, $\lambda$ of matrix $A$, “you take the determinant of lambda times the identity minus $A$ [$|\lambda I – A|$], you get lambda squared plus one equals zero [$\lambda^2 + 1 = 0$], so lambda equals plus or minus $i$ [$\lambda = \pm i$].” Corinne jumped in to emphasize the new aspect with which they were now dealing, “Ah ha! So now we have complex numbers coming in, all right?”
Corinne also provided some technical terminology, “This is called the characteristic equation. [$\lambda^2 + 1 = 0$] The equation for lambda is lambda squared plus one is equal to zero.” Here she simply told the students something that she wanted them to know. She did not expect the small groups to have intuited the technical name on their own.
Next Corinne reiterated the result, “And that has solutions, lambda equals plus or minus $i$. [$\lambda = \pm i$] The eigenvalue, this is the first example you have of eigenvalues that are complex.” When a student asked a question about its relation to yesterday’s discussion) [00:25:32:00], she chose to delay responding with a simple request, “Let him finish.”
The presenter for group one then continued by stating how they had found the eigenvectors, “So then you have $A$ ket $v$ equals lambda ket $v$. [$A\vert v\rangle = \lambda\left\vert v \right\rangle$] So we take $A$ and multiply it by $x$, $y$ and we set that equivalent to $i$ multiplied by $x$, $y$ and as you can see by this beautiful work with the equations [points to $-y= ix$; $x=iy$; $x=1$; $y=-i$] $v$ is a vector that is one, minus $i$ [points to $v$] All right. Following a similar operation with minus $i$, we get one and $i$.” After stating that “these are our eigenvectors,” the student re-described them in normalized form.
This is an example of a student gaining experience in speaking this specialized language publicly. In contrast to listening to a lecture, making such presentations involves developing professional judgment about what to say, such as how much detail to include. Some students, for example, report on every single calculation that they make and some students do not report on any. In this case, the student showed the equation that he was solving and when the algebra was straightforward, he just stated the answer.
At this point, Corinne interjected a request, “So the first eigenvector that you got, before you normalized it, was one, minus $i$. Can you draw that on the board for me?” This prompt asked the student to do something that in general cannot be done and initiated a conversation about what the implications are of having complex components in an eigenvector.
Although Corinne had intended to get students trying to think about complex vector spaces, she does not remember planning to ask this specific question. However, a check of the video of this wrap-up discussion during an earlier year showed a student asking a question about graphing complex eigenvectors. A memory of this question in this context may have cued Corinne’s spontaneous decision here to get students to extend their understanding of real vectors, which can be drawn on the board, to complex vectors, which in general cannot. Corinne considers the conversation that followed an example of a particularly productive classroom conversation because different students had different ways of coming to terms with the complication that was posed and as the students expressed their various different ways of thinking about it other students in the class heard enough alternative explanations that hopefully at least one resonated with them.
In response to Corinne’s request, the first group’s presenter drew two perpendicular axes on the blackboard and labeled them $x$ (horizontal) and $i$ (vertical). Next he drew an arrow downward and to the left into the third quadrant (see Figure 4).  Another student proposed a correction that caused the presenter to erase the arrow and redraw it upward and to the left into the second quadrant. After further coaching from a classmate, he erased the second arrow and drew a third version downward and to the right into the fourth quadrant.
Another student proposed a correction that caused the presenter to erase the arrow and redraw it upward and to the left into the second quadrant. After further coaching from a classmate, he erased the second arrow and drew a third version downward and to the right into the fourth quadrant.
After the first group’s presenter turned and looked at Corinne for confirmation, she deflected the authority of judging right answers to the students by asking “Do you all agree with that?” A student responded, “You need four dimensions for more-than-one-component vectors.” Apparently she had remembered and understood a related discussion two days earlier. Corinne elaborated this statement, “You need four dimensions. [Student J] says that you need four dimensions and you've only got two” and then queried, “So why do you need four dimensions?” Several students contributed their ideas in overlapping talk. Corinne affirmed these with, “Absolutely! This is a two dimensional piece of a four dimensional space.”
To explore this issue explicitly, Corinne asked the student at the board, “So what are your axes? The one that you have this way (gestured horizontally with right arm), what did you plot on that?” and clarified her question, “Which piece of information?” With prompting, the student then articulated that he had represented “the real part” of the first entry of the vector $\pmatrix{1\cr -i}$ on the horizontal axis and “the imaginary part of the second entry” of the vector $\pmatrix{1\cr -i}$ on the vertical axis.
Corinne commented on the zero imaginary component of the first entry and the zero real component of the second entry and then quipped, “you lucked out.” Several students chuckled at her use of this colloquial phrase to describe the situation in which the two dimensional representation that the student had drawn was appropriate only because two of the four dimensions were zero. Such chuckles were an indication that at least these students were following the argument enough to recognize the attempt at humor,
After reiterating the issues clearly, Corinne shifted attention to interpreting what was happening: “The group that did this back on Tuesday, you said there were no vectors that were unchanged but you weren't thinking about imaginary vectors. Right? You were working with just arrows that you could draw with a real part on the first part and a real part on the second part and that's the only entries they had.” Affirming a student’s comment, Corinne continued, “That's a rotation. If you do a rotation in two dimensions, every vector rotates if you're thinking about just the real ones.” She reached for a small white board and demonstrated a rotation.
Then she articulated the primary point that she wanted the students to understand from this problem, “but there are eigenvectors to such a matrix, they're just complex. So in the four dimensional space, there are some things that don't get rotated.”
Representing a Generalized Sense of Direction: Group 2 [00:30:23.28] – [00:33:37.19]
The presenter for the second group began by pointing to the matrix at the top left of his group’s white board, “so we had this one right here: zero, one, one, zero.” This group’s matrix and solution are shown in Figure 5.
Corinne again interrupted to get the class to anticipate what the answer was going to be by asking “Who had this one on Tuesday?” After a long pause amid low student talk and laughter, she relented, “Nobody's going to admit to it? Okay. So everybody then, what, what does this matrix do to real vectors?” A student responded, “It reflects” and Corinne pressed for more specifics, “It reflects along what line?” Students offered, $y=x$, $y$ axis” Corinne responded, “It reflects along $y =x$” and asked the next appropriate question for reviewing this kind of problem, “So what do we expect to be eigenvectors?” and a student answered, “$y=x$; one, one.”
Having reviewed the findings from the geometric explorations on Tuesday, Corinne confirmed, “One, one. Okay. Go ahead.” The presenter for group two made a gesture that his classmates interpreted with laughter, as they recognized that his main result had just been reported and now he had little to say. Corinne stepped in to defend this situation with a comment directed toward their professional development as practicing physicists, “Before you set off doing a calculation, ask yourself if you know the answer. Okay, because it really helps you to keep from making algebra mistakes if you know what you're supposed to be getting.”
The presenter for group two responded with a comment about his perception of the nature of physics, “I thought that was the whole point of physics. You're supposed to think you get something and you get something totally different and you make sense of it.” As his classmates laughed, he added, “And then you get the Nobel Prize.” He was acknowledging the contradiction students frequently experience between physicists’ emphasis on developing physical intuition and students’ surprise at physicists’ interpretation of many phenomena. Amid more laughter, Corinne responded, “Lots of time in classroom physics you don't get a Nobel Prize.”
The presenter for group two then turned to the serious business of presenting his group’s work, “So, ah, run through the math and again our lambda values are one and negative one, so our vectors are one, one and one, negative one [points to vertical vectors: $$\vert v_1\rangle = \pmatrix{1\cr 1} \qquad\hbox{and}\qquad \vert v_2\rangle= \pmatrix{1\cr -1} $$
Corinne responded by requesting an elaboration, “Okay. So you have one that is along $x$ $y$, along the line $x = y$, but what's that other one?” When the presenter responded, “Ah that is the one that is 90 degrees perpendicular to,” Corinne said softly, “pi over two” and the student corrected himself, “pi over two, same thing’ with a laugh and continued, “Ah, it's pi over two shifted.” However, he encountered some uncertainly “cause eigenvalues can change” and thinking on his feet concluded, “well, it's just a rev - it's a negative of itself, it's ninety, ah, pi shifted from itself, which makes it just the opposite.” He seemed to be choosing his language very carefully to avoid saying that this was an eigenvector because he did not seem to be sure what “changing direction” meant. In reflecting upon the video of this interaction, Corinne noted that the issue is that common everyday language says that the negative of a vector points in the opposite direction but in technical language one would say that the negative of a vector points in the ‘same’ direction but it’s length is multiplied by minus one. This example provided a good opportunity to have that discussion with the students.
Again Corinne requested a graphical representation, “so can you draw those?” As shown in Figure 6, the presenter for group two drew two axes and a dotted line representing y = x, drew an arrow from the origin along $y=x$ into the first quadrant for the first eigenvector, [$v_1 =\pmatrix{1\cr 1}$ ] and then drew an arrow from the origin to the fourth quadrant, for the second eigenvector [$v_2 =\pmatrix{1\cr -1}$]. Corinne offered an interpretation, “So one, one goes to itself and one, negative one goes to minus itself.” [$A\vert v_1\rangle = 1\vert v_1\rangle$] and [$A\vert v_2\rangle = -1\vert v_2\rangle$]. The presenter for group two turned toward Corinne and nodded. Corinne continued, “Good. So this is why we want to include multiplication by negative one as still being, pointing in the same direction in quotes [makes signs for quotation marks with both arms raised] our generalized sense of direction, because it is a solution to the eigenvalue equation.”
Monitoring Algebraic Accuracy and Interpreting a Result: Group 3 [00:33:37.19]- [00:37:15.21]
The presenter for the third group began by pointing to the matrix they had used and saying, “So the thing in purple is $A$ three. Our matrix is negative one, zero, zero, negative one.” Group 3’s matrix and solution are shown in Figure 7.
The presenter rapidly described her group’s calculations and presented their result, “our lambda value is one” and holding up one finger for emphasis, she reiterated, “we only have one.” Modeling what a professional would ask if anticipating two solutions, Corinne questioned that result, “How can that be if it was a quadratic equation?”
The presenter moved her hand over their equation [$(\lambda -1)(\lambda -1) = 0$] and said, “It was the same thing.” Corinne supplied terminology for that situation, “You got a repeated root,”<yes>, reviewed components of the equation, “It was lambda minus one times lambda minus one [student nodded yes], and verified the result, “You got lambda equals one twice.” <yes> By correctly pointing at the equation and going back and forth with her hand, the student had signaled that she understood that there was a duplication in the equation but she did not have words for it so Corinne provided the words 'there's a repeated root.' While reflecting on the video of the wrap-up discussion, Corinne noted that the ability to provide students with correct language for a concept that they are seeing is a valuable part of these wrap-up discussions. That opportunity only occurs if some of class time is devoted to student presentations rather than lecture.
The presenter then explained, “So you do the thing you're supposed to do to find vectors, $A$ times $x$ $y$ and lambda times $x$ $y$ and you solve and we got $y$ equals negative two $x$ so it made $x$ one,[points to $x=1$] and $y$ is equal to negative two. Corinne chose to challenge this result, “Okay. I don't believe your algebra” and worked with the student to identify the problem, “Go where you said lambda equals one, where you have a circle <yes> go up a line, up one from there, you have lambda minus one times lambda minus one, [$(\lambda -1)(\lambda -1)$], go up two lines from that, you have minus one minus lambda times minus one minus lambda, [$(-1-\lambda)(-1-\lambda)$] I don't think those are the same equations. <okay> How did you get from one to the other?”
As students began to offer comments, Corinne walked to the board and discussed an algebraic procedure that she had seen many students do, of multiplying out a factored quadratic and then using the quadratic formula to factor again, but making a mistake. Here there had been a sign error, so the answer should have been that the eigenvalues were minus one. [$A\vert v\rangle = -1\vert v\rangle$]
Having corrected the algebra, Corinne raised the issue that she had designed this problem to highlight, “But here's this matrix, minus one times the identity, what does that operation do?” and repeated, “It's negative one times the identity, so what does it do to a vector?” In overlapping talk, students offered answers that Corinne confirmed, “It's a pi rotation, or which just ends up taking everything to minus itself.”
Then Corinne pressed for the main idea she wanted them to realize, “so if takes everything to minus itself, what are the eigenvectors?” She emphasized, “Everything! Okay? So you got $x$ equals one and $y$ equals minus two for example but actually EVERYTHING is an eigenvector.”
Noticing and Defining Degeneracy: Group Four [00:37:15.21] - [00:43:17.28]
As Corinne returned to her seat near the back of the room, she made a decision to call on a particular group, one that she wanted to follow the previous example, so that the class could continue the conversation they were having. The presenter for group four began in the same way as the others, by identifying the matrix his group had used, “Our matrix was negative one, zero, zero, zero, negative one - this thing here” he finally said as he pointed to a three by three matrix with zeros everywhere but on the diagonal. Group 4’s matrix and solution are shown in Figure 8.
Corinne took this opportunity to coach his use of language, “Lots of times people, if they have a matrix that has things only on the diagonal, instead of saying minus one, zero, zero, zero, minus one, you got tired right? and quit in the middle? <yeah> <laughter> which is what everybody does. If it's just diagonal, the convention is to say it's diagonal and you just read off the diagonal ones, and then everybody knows its diagonal.”
While reflecting upon the video, Corinne noted that there are so many new concepts at this level that the students do not know how to articulate them clearly for themselves and so in the classroom she does a lot of talking, but in response to what students say - here's a way of saying this, there's a way of saying this, try phrasing it this way. This active shaping of ways of speaking could occur because she provided many opportunities for the students to do the talking.
The presenter accepted her suggestion and stated, “It's diagonal, with one negative one one.” When she asked him how that compared with the previous matrix, he answered immediately, “It's the same matrix except it's three by three with a one,” and pointed to the one in the bottom right corner. Corinne confirmed his response, “So that upper left corner is the same as what [Student J] just did,” and stated explicitly the reason for her decision, “That's why I wanted to do this one next.’
At this point, Corinne addressed the entire class, “Okay. Now. So what do you all expect here? Do you have any expectations?” In reflecting upon these questions while watching the video, Corinne noted that although these questions match what she had asked at this point in the earlier presentations, she apparently also was wondering them for herself, as an instructor thinking aloud in the moment, pondering whether or not her students would have any expectations for this matrix. After several students responded, she asked for a repeat, “What are you saying, say that again, what do you expect to happen along the $z$ axis?” and a student replied, “Nothing.” “Nothing,” Corinne confirmed, “you expect the $z$ axis to be unchanged” and picking up on another student’s comment, she exclaimed, “and therefore you expect it to be an eigenvector, yes!”
The presenter then articulated an inference he was making based upon the previous student’s problem, “If I didn't do this beforehand and then I saw hers,” while pointing to the previous student’s whiteboard, “and then I started to do this, I'd expect one of my eigenvalues to be their eigenvalue, that's what I'd expect.” This was exactly the kind of thinking that Corinne was attempting to nurture and likely occured because this student had already made the connection between his matrix and the one discussed previously. The video record documented the members of this small group interacting with one another during group three’s presentation when they had realized that the matrix under discussion then was contained within their own.
Corinne acknowledged this expectation by repeating it explicitly and re-stating the eigenvalue group three should have gotten, minus one. Next the presenter pointed to calculations on his group’s whiteboard and summarized their results, “We got eigenvalues of negative one, which repeats itself, and one.” Corinne confirmed this by making the connection again to the previous group’s results, “So you got lambda equals minus one, lambda equals minus one, just like [Student J]'s group, and one.”
Then the presenter for this group went on to discuss the eigenvectors for these eigenvalues, “Doing lambda equals one first, our equation is negative $x$ equals $x$, [$ -x= x$], negative $y$ equals $y$, [$-y = y$] and $z$ equals $z$ [$z=z$] and our eigenvector for it to solve for all three of these equations is any scalar times zero, zero, one. He pointed to the white board where his group had written $|\vert v\rangle = \alpha\pmatrix{0\cr 0\cr 1}$ where they had used the symbol $\alpha$ to represent any scalar number.
To emphasize what this presenter had just explained, Corinne stated explicitly, “This is one of the tricky things I wanted you all to see. If you get the equation minus $x$ equals $x$ as one of your equations when you're solving for the eigenvector, what are the solutions of minus $x$ equals $x$?” After several students responded, “Zero,” Corinne commented in a way she intended to be humorous but also emphatic, “Zero, Okay? Zero is a number, it's a possible answer!” As students smiled, she continued, “And you may well get zero. One of the components has to be zero. So if you see minus $x$ = $x$ don't freak and say there are no solutions. There IS a solution, $x$ = zero.” Her emphasis here came from many experiences with students, even in this advanced physics course, who think of zero as meaning ‘no answer’ rather than as an answer with the numerical value of zero.
The next point to be made concerned the interpretation of this eigenvector $\pmatrix{0\cr 0\cr 1}$. Corinne prompted this with “So for your lambda equals one you got zero, zero, one, which is?” A student responded, “k hat,” the name they had been using for a unit vector along the $z$ axis. Corinne then summarized the interpretation she wanted them to understand, “k hat. Absolutely and you got any scalar multiple of k hat, so any vector that lies along the $z$ axis, is an eigenvector with eigenvalue? <one> one. It's not stretched, it's not rotated, it doesn't change at all. “
The presenter then went on to discuss the eigenvector for the eigenvalue negative one, “For lambda equals negative one, we got negative $x$ equals negative $x$ [$-x = -x$], negative $y$ equals negative $y$ [$-y = -y$] and $z$ equals negative $z$ [$z = -z$] so our eigenvector is 1, 1, 0 times a scalar.”
What followed was an interchange that elaborated one of the main points that Corinne wanted to develop during this session:
Corinne: Okay. So if you've got negative $x$ equals negative $x$, $x$ can be?
Student T: Anything
Corinne: Anything and you also got $y$ to be?
Student T: Anything
Corinne: So you picked one, one, zero,
you picked the same anything for $x$ as you did for $y$
The presenter (Student T) interpreted this remark to mean there could be another possibility:
Student T: So you're saying $y$ could be something different from $x$
Having established this context for articulating a major issue, Corinne cautioned:
$y$ could be something different from $x$ and you do have to be careful in this sense that if you get several different things that can be anything, they can be different anythings, don't necessarily pick them to be the same.
Moving to the front board, she shared her own approach as a practicing physicist to this issue:
Now I will actually myself to remind myself of this, I will write them as,
I will write it as anything, anything, zero
[writes vertical vector anything, anything, zero]
This is an example of a strategy Corinne often uses, writing out words in formats where symbols would be expected as a way to emphasize that symbols have meanings, that as practicing physicists her students should be thinking in words as they read and write in symbols.
In reflecting upon this interaction while watching the video, Corinne noted that this is the sort of moment that may be more effective for this student and possibly for other members of the class than straight lecture. He had chosen one, one, zero and he was now realizing that he did not need to choose those two things to be the same. This is a clear example of dragging something out of a student rather than letting him discover it for himself but it was motivated by work that the student himself did. If she had just tried to do this with lecture and said the solutions of these equations are anything, anything, zero, most of the students in the class may have missed the point.
Turning to the class, Corinne asked the students to consider the implications of getting repeated eigenvalues:
but how many eigenvectors are there with the eigenvalue minus one?
After a student responded, “infinite,” Corinne elaborated:
There are an infinite number of eigenvectors.
There are even an infinite number of normalized eigenvectors.
So here we have two cases, where we have minus one, minus one on the diagonal
(pointing to Group 3’s whiteboard)
and minus one, minus one on the diagonal (pointing to Group 4’s white board)
and we got MORE eigenvectors than we were expecting,
There wasn't just one
A student suggested a way to express this: “alpha,1, 0, 0 plus beta zero, one, zero” and Corinne responded:
Yes so you can write it as, the eigenvectors as, that's a really nice way to write it, alpha one, zero plus beta zero, one for any values of alpha and beta, $$\alpha \pmatrix{1\cr 0} + \beta \pmatrix{0\cr 1}$$ all of them can be written this way [points to board].
Corinne added a third zero to each, to represent three dimensions and interpreted the result:
So this is $x$ hat or $i$ hat [points to $\alpha \pmatrix{1\cr 0\cr 0}$] and $j$ hat [points to $\beta \pmatrix{0\cr 1\cr 0}$]
so any vector that lies in the $x$ $y$ plane, that whole plane full of them,
[moving arms to form a horizontal plane]
is an eigenvector with eigenvalue minus one.
Then she concluded what had become a mini-lecture with the definition of a term she wrote on the board:
This is a situation that's called degeneracy
and it happens any time you have a repeated eigenvalue.
As Corinne turned to point to the two white boards with repeated eigenvalues, a student asked “Does this have a degeneracy of two?” She answered, “This has a degeneracy of, yes, it’s a two dimensional, the degeneracy gives you a two dimensional, it's called an eigenspace and we'll talk more about this tomorrow.”
The discussion about degeneracy, one of the main goals of this compare and contrast activity, presented information within the context of student engagement. The small group activities and presentations not only provided opportunities for students to gain experience in expressing their ideas but also enabled them to hear about nuances in both speaking and thinking physics in contexts in which they were deeply engaged and ready to learn.
Interpreting Diagonal Matrices: Group 5 [00:43:17.28] -
Acknowledging that class was almost over, Corinne asked for the group “with $a$’s and $d$’s” to “give us a thirty second presentation” and returned to her chair in the back of the room.
The presenter for this group began by using the language about diagonal matrices that Corinne just had coached during the presentation by group 4, “So we had a diagonal matrix with $a$ and $d$, so we went through and we used the general equation to solve for the eigenvalues which were $a$ and $d$ cause you know all these reasons anyways” as he waved his hands over various equations. Group 5’s matrix and solution are shown in Figure 9.
In spite of the limited time available, Corinne intervened, “Wait! Are those reasons obvious?” The student responded, “Well, solving the quadratic [ $(\lambda - a)(\lambda -d) = 0$], Liz pointed out you don't really need to solve it when you know that $a$ minus $a$ is zero and $d$ minus $d$ is zero.”
Corinne then presented a challenge to emphasize what she wanted students to learn,
“So suppose you had a 27 by 27 matrix and it was diagonal?” After the presenter mocked being shocked, Corinne repeated her challenge, “Suppose you had a 27 by 27 matrix and it was diagonal, what would its eignvalues be?” One of the students mentioned the diagonal, and Corinne confirmed, “All the elements on the diagonal.”
Amid the amusement of his classmates at the absurdity of dealing with a 27 by 27 matrix, the presenter pressed on in explaining what they had done. He concluded with, “The only case that $d$ $y$ equals $a$ $y$ is $y$ equals zero and therefore $x$ can equal anything and then we just did the exact same thing on the other one so we got our vectors one, zero and zero, one.”
Corinne concluded this problem by summarizing what she wanted them to realize:
Any time you have a diagonal matrix, the eigenvalues are just the elements of the diagonal and the eigenvectors are one, zero and zero, one. They're $i$ hat and $j$ hat, and $k$ hat, They're the really nice eigenvectors. It's trivial. You will come to know and love diagonal matrices.
Then she closed the class with , “All right. There's a homework assignment up here and we'll see you tomorrow. Remember there's a quiz and you will have to do this and it will not be such a tricky one.” References
Hymes, D. (1972). Models for the interaction of language and social life. In J. Gumperz & D. Hymes (Eds.), Directions in sociolinguistics: The ethnography of communication (pp. 35-71). New York: Holt, Rinehart & Winston.
Philipsen, G. & Coutu, L. (2004). The Ethnography of Speaking. In K. L. Fitch & R. E. Sanders (Eds.), Handbook of language and social interaction (pp.l 355-380. Mahwah, NJ: Lawrence Erlbaum.
van Zee, E. H. & Minstrell, J. (1997a). Reflective discourse: Developing shared understandings in a high school physics classroom. International Journal of Science Education, 19, 209-228.
van Zee, E. H. & Minstrell, J. (1997b). Using questioning to guide student thinking. The Journal of the Learning Sciences, 6, 229-271.