You are here: start » courses » order20 » vforder20 » vfcalculating
Calculating Potentials
Prerequisites
Students should be able to:
- Find the electric potential from a system of discrete point sources.
- Write the difference vector between two vectors (and its magnitude).
- (Optional) Write charge densities in terms of delta functions.
- Compute line integrals.
- Find power series approximations.
In-class Content
Lecture: Electric Potential
Students may be familiar with the iconic equation for the electric potential (due to a point charge): $$\text{Iconic:} \qquad V=\frac{1}{4 \pi \epsilon_0} \frac{Q}{r}$$ With information about the type of source distribution, one can write or select the appropriate coordinate independent equation for $V$. For example, if the source is a line of charge: $$\text{Coordinate Independent:} \qquad V=\frac{1}{4 \pi \epsilon_0} \int\frac{\lambda | d\vec r' |}{| \vec r - \vec r' |}$$ Looking at symmetries of the source, one can choose a coordinate system and write the equation for the potential in terms of this coordinate system. Note that this step is often combined with the following step, though one may wish to keep them separate for the sake of careful instruction. $$\text{Coordinate Dependent:} \qquad V=\frac{1}{4 \pi \epsilon_0} \int\frac{\lambda |ds'\ \hat s + s'\ d\phi'\ \hat \phi + dz'\ \hat z|}{| s'^2 + s^2 +2ss' \cos(\phi-\phi') + z^2|}$$ Using what you one about the geometry of the situation, one can possibly simplify the numerator. For example: $$\text{Coordinate and Geometry Dependent:} \qquad V=\frac{1}{4 \pi \epsilon_0} \int\frac{\lambda s'\ d\phi'}{| s'^2 + s^2 +2ss' \cos(\phi-\phi') + z^2|}$$ Emphasize that “primes” (i.e., $s'$, $\phi'$, $z'$, etc.) are used to indicate the location of charge in the charge distribution.
Lecture: Chop, Calculate, and Add
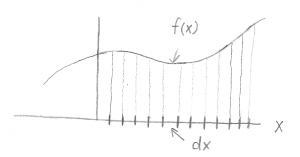
- To find the area under a curve, one may chop up the x-axis into small pieces (of width $dx$). The area under the curve is then found by calculating the area for each region of $dx$ (which is $f(x) dx$) and then summing up all of those areas. In the limit where $dx$ is small enough, the sum becomes an integral.
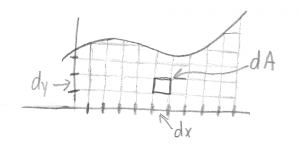
- One could also find the area under a curve by chopping up both the x- and y-axes (chop), calculating the area of each small area under the curve (calculate), and adding all of those together with a double sum or double integral.
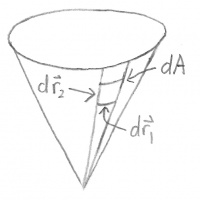
- This approach can be used to find the area of a cone, where the 'horizontal' length of each area is $r d\phi$ and the 'vertical' length is $dr$, giving an area of $dA = r d\phi dr$. It is important to make sure that the limits of integration are appropriate so that the integrals range over the whole area of interest.
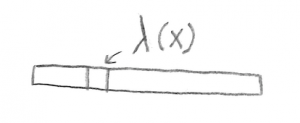
- If one wants to calculate something other than length, area, or volume, such as if one sprinkled charge over a thin bar, then chop, calculate, and add still works. Again, chop the bar up into small lengths of $dx$. Then calculate the charge $dQ$ on each length ($dQ = \lambda dx$), and add all of the $dQ$s together in a sum or integral.
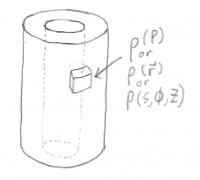
- This also works for calculating something (such as charge) over a volume. For a thick cylindrical shell with a charge density $\rho(\vec r)$, chop the shell into small volumes of $d \tau$ (which will be a product of 3 small lengths, e.g. $d \tau = r d\phi\ dr\ dz$), multiply this volume by the charge density at each part of the shell (defined by e.g. $r, \phi,$ and $z$), and add the resulting $dQ$s together.
Activities
- Lines of Charge (Lecture: 30 min)
Homework for Symmetries
- (FiniteDisk)
Starting with the integral expression for the electrostatic potential due to a ring of charge, find the value of the potential everywhere along the axis of symmetry.
Find the electrostatic potential everywhere along the axis of symmetry due to a finite disk of charge with uniform (surface) charge density $\sigma$. Start with your answer to part (a)
Find two nonzero terms in a series expansion of your answer to part (b) for the value of the potential very far away from the disk.
- (InfiniteDisk)
Find the electrostatic potential due to an infinite disk, using your results from the finite disk problem.
- (PotentialConeGEM227)
A conical surface (an empty ice-cream cone) carries a uniform charge density $\sigma$. The height of the cone is $a$, as is the radius of the top. Find the potential at point $P$ (in the center of the opening of the cone), letting the potential at infinity be zero.
- (WritingII)
Using the handout “Guiding Questions for Science Writing” as a guide, write up your solution for finding the electrostatic potential everywhere in space due to a uniform ring of charge. Be sure to include a series expansion along one of the axes of interest.