You are here: start » courses » lecture » pplec » pplecnwellhamil
Hamiltonian for the n-well System (20 minutes)
- It is recommended that students first see the analysis of a 2-well system.
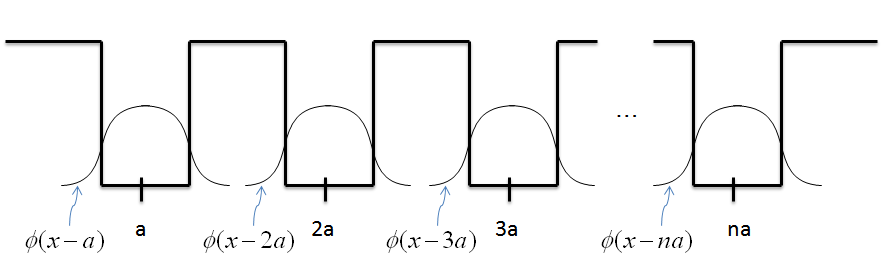
- Let's expand our discussion of periodic wells to a system with n-wells, as seen below.
Recall that the Hamiltonian for our 2-well system had the form
$$H \; = \; \left[\begin{array}{cc} \alpha & \beta \\ \beta & \alpha \\ \end{array}\right] \; = \; \left[\begin{array}{cc} \langle 1 \vert H \vert 1 \rangle & \langle 1 \vert H \vert 2 \rangle \\ \langle 2 \vert H \vert 1 \rangle & \langle 2 \vert H \vert 2 \rangle \\ \end{array}\right] \; \; . $$
Notice how we used the basis states to represent each term in the Hamiltonian. The same process will work for a system with N-wells, where now there will be n-basis states with the form
$$\phi(x-a) \; \dot{=} \; \vert 1 \rangle $$ $$\phi(x-2a) \; \dot{=} \; \vert 2 \rangle $$ $$.$$ $$.$$ $$.$$ $$\phi(x-na) \; \dot{=} \; \vert n \rangle $$
Note that using this strategy will only be an approximation, but it works well.
- Now, let's create our our n $x$ n Hamiltonian for our n-well system using the basis states.
$$H \; \dot{=} \left[\begin{array}{cccc} \langle 1 \vert H \vert 1 \rangle & \langle 1 \vert H \vert 2 \rangle & \langle 1 \vert H \vert 3 \rangle & \dots\\ \langle 2 \vert H \vert 1 \rangle & \langle 2 \vert H \vert 2 \rangle & \langle 2 \vert H \vert 3 \rangle & \\ \langle 3 \vert H \vert 1 \rangle & \langle 3 \vert H \vert 2 \rangle & \langle 3 \vert H \vert 3 \rangle & \\ \vdots & & & \ddots \\\end{array}\right] \; \; $$
We now have the Hamiltonian; all we must do now is find the value of each entry. Let's look at the entries in classes.
- Entries on the diagonal:
Let's expand the first two entries out into function notation to compare them.
$$\langle 1 \vert H \vert 1 \rangle \; = \; \int \phi^{*}(x-a)H \phi(x-a) dx \; \; , $$
$$\langle 2 \vert H \vert 2 \rangle \; = \; \int \phi^{*}(x-2a)H \phi(x-2a) dx \; \; . $$
Notice that the integrals are identical; the only difference is that the function is shifted to the right by one step. The same pattern will continue across all entries on the diagonal, so
$\langle n \vert H \vert n \rangle = \alpha \; \; . $$
- Entries neighboring the diagonals:
Let's first look at the overlap function of the first well onto the second well.
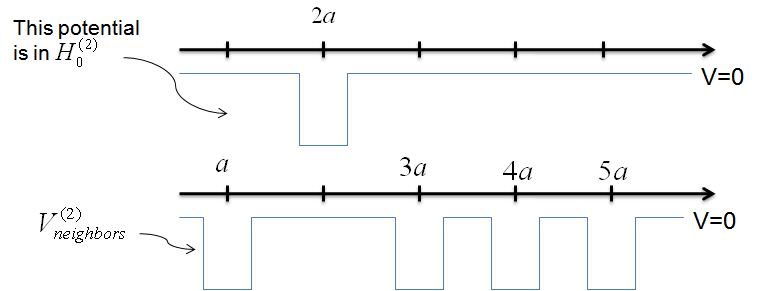
$$\langle 1 \vert H \vert 2 \rangle = \langle 1 \vert H_{0}^{(2)} + V_{neighbors}^{(2)} \vert 2 \rangle \; \; , $$
where $H$ is the full Hamiltonian, $H_{0}^{(2)}$ is the Hamiltonian for the atom at $2a$ alone, and $V_{neighbors}^{2}$ contains the potential functions of each well that neighbors the atom at $2a$.
Expanding out the Hamiltonian is a crucial step: If we multiply the bras and kets through the expression, we get
$$\langle 1 \vert H \vert 2 \rangle = \langle 1 \vert H_{0}^{(2)} \vert 2 \rangle + \langle 1 \vert V_{neighbors}^{(2)} \vert 2 \rangle \; \; . $$
Using the energy eigenvalue equation, we know that $H_{0}^{(2)} \vert 2 \rangle = E_{2} \vert 2 \rangle$. Since the energy is a constant, we can factor it out to have
$$\langle 1 \vert H \vert 2 \rangle = E_{2} \langle 1 \vert \vert 2 \rangle + \langle 1 \vert V_{neighbors}^{(2)} \vert 2 \rangle \; \; , $$
$$\langle 1 \vert H \vert 2 \rangle = \langle 1 \vert V_{neighbors}^{(2)} \vert 2 \rangle \; \; . $$
Repeating the process by analyzing the second well's overlap onto the first well will give
$$\langle 2 \vert H \vert 1 \rangle = \langle 2 \vert V_{neighbors}^{(1)} \vert 1 \rangle \; \; . $$
Both entries will resolve into the same integral and ultimately yield the same value.
$$\langle 2 \vert H \vert 1 \rangle = \langle 1 \vert H \vert 2 \rangle = \beta \; \; . $$
- Entries with a well spacing of $2a$ or greater:
Let's look at the first well's overlap onto the third well. Performing the same analysis as with the neighboring wells, we find that
$$\langle 1 \vert H \vert 3 \rangle = \langle 1 \vert V_{neighbors}^{(3)} \vert 3 \rangle \; \; . $$
To find the value for this entry, we would have to evaluate the integral
$$\langle 1 \vert H \vert 3 \rangle = \int \phi^{*g}(x-a) V_{neighbors}^{(3)} \phi^{g}(x-3a) dx \; \; . $$
However, if we look at the spacing in the wells, the ground state functions for the first and third well hardly overlap.
Add image: pplecnwellhamil3
The separation will result in the integral being essentially zero.
Putting all of the entries that we found back into the Hamiltonian gives:
$$H \; \dot{=} \left[\begin{array}{ccccc} \alpha & \beta & 0 & 0 & \dots\\ \beta & \alpha & \beta & 0 & \\ 0 & \beta & \alpha & \beta & \ddots \\ 0 & 0 & \beta & \alpha & \ddots \\ \vdots & & \ddots & \ddots & \ddots \\ \end{array}\right] \; \; . $$
Again, we have made several approximations to arrive at this Hamiltonian. Nevertheless, it's something we can use approximate the energies of eigenstates for larger well systems.