You are here: start » courses » lecture » pplec » pplecapproxbe3dlat
Approximating the Internal Energy for a 3-D Lattice (30 minutes)
Time permitting, this lecture also converts well into an activity for students to tackle in small groups.
* Before performing this lecture, it is recommended that students first Approximate the Internal Energy for a 1-D Chain.
- Present the students with the following prompt:
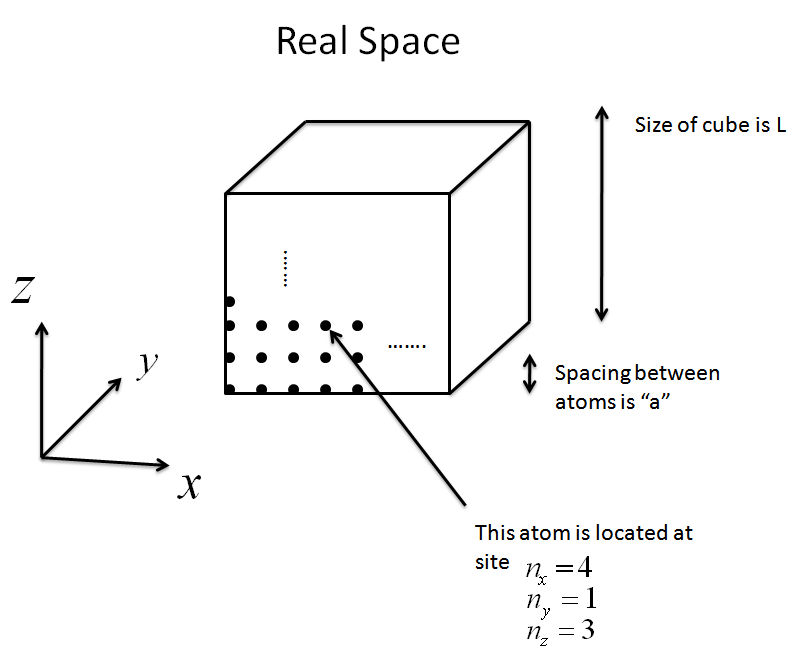
A 3-dimensional cube with side length $L$ is filled with a total of $N$ atoms that have spacing $a$ between them.
Find the total energy stored in the lattice when:
a) $T > \frac{\hbar \omega_{max}}{k_{B}}$
b) $T < \frac{\hbar \omega_{max}}{k_{B}}$
- Solutions
a) Just as with the one-dimensional case, the energy stored in the lattice above the “freeze out” zone can be estimated using the equipartition theorem.
$$U_{tot}=\left(\text{Total # modes}\right)\left(k_{B}T\right)=3Nk_{B}T \; \; . $$
b) Before we can find the total energy stored in the cube, we need to properly enumerate the envelope functions that are allowed inside the cube. There are two key things to remember when doing this:
- The boundary conditions of the allowed normal modes in the x,y, and z directions must all be satisfied. That is, the general envelope function must be zero at all points on the cube's edge.
- This cube is essentially a bunch of one-dimensional monatomic chains stacked on each other and with different orientations; because of this, we should expect that the envelope function should show some similarity to the 1-dimensional envelope function we've used in the past, which had the form $$x(t)=C \sin{kna} \; \; .$$
The envelope function that satisfies these conditions is
$$\delta_{n_{x}, n_{y}, n_{z}}=A \sin{\left(k_{x}n_{x}a\right)} \sin{\left(k_{y}n_{y}a\right)} \sin{\left(k_{z}n_{z}a\right)} \; \; , $$
where $n_{x}$, $n_{y}$, and $n_{z}$ all define the location of the atom in real space, while $k_{x}$, $k_{y}$, and $k_{z}$ all define what the wave number is for the envelope function in the x,y, and z orientation.
- Just like the boundary conditions for the 1-D case, we are also limited to only certain values for $k_{x}$, $k_{y}$, and $k_{z}$.
$$k_{x}=\frac{\pi}{L}, \frac{2\pi}{L}, \frac{3\pi}{L},…$$
$$k_{y}=\frac{\pi}{L}, \frac{2\pi}{L}, \frac{3\pi}{L},…$$
$$k_{z}=\frac{\pi}{L}, \frac{2\pi}{L}, \frac{3\pi}{L},…$$
This will be very important when we try to find all of the modes that are not frozen out for the cube.
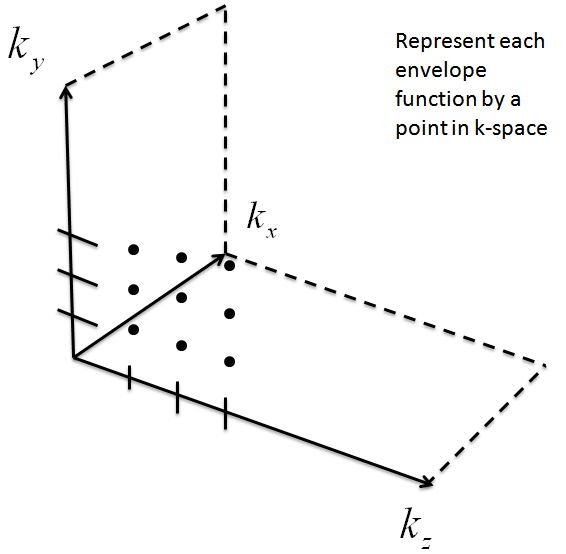
- How do we find the number of modes that have not frozen out? In the one-dimensional case, we drew a bar line, represented each envelope function's wave vector on the bar, and worked to determine the number of modes with lower wave vectors than $k_{freeze}$. We will now use the same premise, but in three-dimensional k-space.
Just like in the 1-D case, each point in k-space represents the envelope function $\delta$ that has the wave vectors $k_{x}$, $k_{y}$, and $k_{z}$. The only difference between the three-dimensional case and the one-dimensional case is that we are now looking for all of the normal modes within a volume of radius $k_{freeze}$.
- Now, we're on the hunt for information about $k_{freeze}$. Let's look at the dispersion relation once again. Since the lattice is essentially a stack of one-dimensional chains, we can approximate that the dispersion relation for the cube will be
$$\omega(k)=\omega_{max}\sin{\frac{ka}{2}} \; \; , \; \; \; \; \; \; \; \; \; \; \; k=\sqrt{k_{x}^{2}+k_{y}^{2} + k_{z}^{2}} \; \; .$$
Notice that $k$ looks just like a radius, as we anticipated. We can now approximate that $k_{freeze}$ is small to receive
$$\omega_{freeze} \approx \omega_{max}\frac{k_{freeze}{a}}{2} \; \; .$$
Look familiar? We can also determine what $\omega_{freeze}$ is using the phonon energy relation (just like the 1-D case) to find that
$$\frac{k_{B}T}{\hbar}=\omega_{max}\frac{k_{freeze}{a}}{2} \; \; , $$
$$k_{freeze}=\frac{2}{a}\frac{k_{B}T}{\hbar \omega_{max}} \; \; . $$
- Now, how do we use this expression for $k_{freeze}$ to find the total number of modes that are not frozen out? Remember that $k_{freeze}$ is a radius that contains information about the number of normal modes within on that radial line only; to find the total number of modes in k-space, we have to find the total volume that the radius sweeps out. The volume swept out by the radius is
$$\text{Volume in k-space}=\frac{1}{8}\frac{4\pi}{3}\left(k_{freeze}\right)^{3} \; \; , $$
where the one-eighth is present because we are only looking at positive wave vectors.
- Finally, we can find the number of modes using a very similar approach to the one-dimensional case.
$$\text{# modes}=\frac{\text{Total volume with radius} \; k_{freeze}}{\text{Density of wave vectors inside volume}} \; \; .$$
Inserting the information we have will yield
$$\text{# modes}=\frac{(3)\frac{1}{8}\frac{4\pi}{3}\left(k_{freeze}\right)^{3}}{\frac{\pi}{L}^{3}} \; \; ,$$
$$\text{# modes}=\frac{k_{freeze}^{3}L^{3}}{2\pi^{2}} \; \; , \; \; \; \; \; \; \; \text{where} \; \; \; k_{freeze}=\frac{2}{a}\frac{k_{B}T}{\hbar \omega_{max}} \; \; .$$
Notice the multiplication by a factor of 3; this is a consequence of the system being three-dimensional and being driven in three different fashions. For each mode, there are actually two transverse modes and one compression mode.
- We're almost there; all we have to do is insert the number of modes into the expression defining the energy stored in the crystal. Doing so gives
$$U_{tot}=\left(\frac{2}{a}\frac{k_{B}T}{\hbar \omega_{max}}\right)^{3}\frac{L^{3}}{2\pi^{2}}k_{B}T \; \; .$$
Notice how for the three-dimensional case,
$$U_{tot} \propto T^{4} \; \; , $$
while for the one-dimensional case,
$$U_{tot} \propto T \; \; . $$
- If we wished to do so, we can also plot the specific heat for this crystal cube using the relation
$$C_{v}=\left(\frac{dU_{tot}}{dT}\right)_{v} \; \; . $$