You are here: start » courses » hw » wvhw » wvhwbarrtunn
Homework for Waves
Reflection of a quantum mechanical particle from a potential step
The potential energy part of the Hamiltonian operator (a potential step of height $V_0$) for a system is depicted as a solid line in the energy/position diagram. This is an example of an unbounded system, so there is no condition on the energy eigenvalue. A particle of mass $m$ and energy $E$ is incident from the left. There are 2 cases: $E >V_0$, and $E <V_0$. (As you work through this problem, think carefully about the problem we discussed where a wave in a rope or cable is incident on a different rope or cable. There are important similarities and equally important differences.) 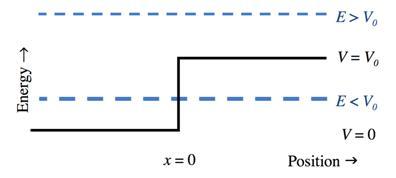
(i) Set up a wave incident from the left, a wave reflected to the left, and one transmitted to the right, so that the total wave function is:
\[\psi \left( {x,t} \right) = \left\{ {\begin{array}{*{20}{c}}{A{e^{i k_1 x}} + B{e^{ - i k_1 x}}}&{x \le 0}\\{C{e^{i{k_2}x}}}&{x \ge 0}\end{array}} \right.\] Verify that these are indeed solutions to the energy eignevalue equation for this problem, provided that
\[{k_1} = \sqrt {\frac{2mE}{\hbar^2}} \]
\[{k_2} = \sqrt {\frac{2m\left( {E - {V_0}} \right)}{\hbar^2}} \].
(ii) What are the boundary conditions that establish the relationships among the coefficients? (iii) The probability to observe the particle reflected is
\[r \equiv {\left| {\frac{B}{A}} \right|^2}\]
(remember we measure probabilities and not amplitudes). Find ${r}$ for both cases: ${E}>{V_0}$, and ${E}>{V_0}$. Also find the probability of transmission ${t}=1-{r}$.
(iv) Interpret your results, and also discuss the limiting cases ${V_0} = 0$, and ${E} > > V_0$.