You are here: start » activities » guides » ppwaveemulate
Navigate back to the activity.
Emulating Waves in a Periodic System : Instructor's Guide
Main Ideas
The atoms in a crystal move about their equilibrium position.
The displacement of an atom from equilibrium can be described by a continuous envelope function.
Evaluating the envelop function at the equilibrium coordinates of an atom tells us the displacement of that particular atom.
Students' Task
Estimated Time: 15
Prerequisite Knowledge
Props/Equipment
- A long blackboard behind the students
- 8 students
Activity: Introduction
Ask for 9 students to volunteer to be atoms inside of a crystal.
When the students are at the front of the class, ask them to organize into a line from shortest to tallest, then stand shoulder-to-shoulder about two feet away from the blackboard.
The instructor draws a straight line on the blackboard just below the students shoulder level. The line will slope upward as it goes behind taller students. Nine tick marks on this line define the equilibrium position of the “atoms”. Define the spacing between tick marks to be length “$a$”.
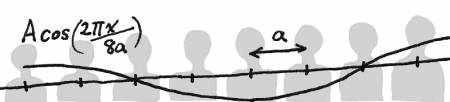
Now the instructor draws the first envelop function. It is a wave $A cos(\frac{2 \pi x}{8a})$. Make the amplitude about 4 inches. Write the equation for the envelope function, as well as drawing the wave. Ask the 9 student atoms to interpret the envelop function by placing their heads at the positions dictated by the envelop function.
Draw another envelop function, $A cos(\frac{2 \pi x}{8 a})$. Make the amplitude about 12 inches. Check that the students can follow this envelop function. This will be more physically demanding and fun for the students to act out.
Now add time dependence to the formula describing the envelop function $A cos(\frac{2 \pi x}{8 a} - \omega t)$. Ask the students to act this out with a frequency of 1 cycle every 8 seconds. Give the students some time to try figuring this out on their own. Encourage input from the audience.
The students will likely need some help with time dependence. For example, the instructor can walk down the line passing one student per second to keep track of a peak in the wave. Note that student 1 and student 9 should be in sync.
Draw the last envelop function, $A cos(\frac{2 \pi x}{4 a} - \omega t)$ and act it out. Keep the wavefront moving at the same velocity (the frequency of each student's/atom's motion will double.
Activity: Student Conversations
The value of the envelope function is physically meaningful at positions a, 2a, 3a…, but what about other positions? This question should lead to a class agreement that we will not attach any physical meaning to the envelop function at other positions.
We just acted out a the collective motion of many particles. Can we classify these motions as normal modes? i.e. were all particles undergoing sinusoid oscillations at the same frequency?
If I wanted to write the envelop wavefunction in the form $cos(kx)$, what values of $k$ were we using? Plot the values of $k$ and the characteristic frequency of the atomic motion on a dispersion relationship.
Activity: Wrap-up
Extensions
In this activity, the coordinate axis was perpendicular to the displacement axis. This is not always the case. It is good to revisit this activity later to emphasis that one-dimensional compressional waves have envelop functions with the same form, but displacement is parallel to the coordinate axis. When displacement is parallel to the coordinate axis we still evaluate the envelop function at a, 2a, 3a…