You are here: start » activities » guides » ppatoms
Navigate back to the activity.
Nine atomic wells: Instructor's Guide
Main Ideas
The wave state of an electron in a periodic can be approximated as a linear combination of atomic orbitals (LCAO). The LCAO states have physical similarities with the normal modes of a periodic system.
The coefficient of each atomic orbital in an LCAO state can be described by an envelope function.
Evaluating the envelop function at the center of a unit cell tells us the coefficient of the atomic orbital associated with the particular unit cell.
Even though the envelop function is continuous, we are only concerned with the value of the envelop function at discrete points in space.
Students' Task
Estimated Time: 15 minutes
Act out the time evolution of two different LCAO states.
Prerequisite Knowledge
This activity is designed to complement "Emulating Waves in a Periodic System".
Props/Equipment
- Nine student volunteers
- A long blackboard behind the students.
Activity: Introduction
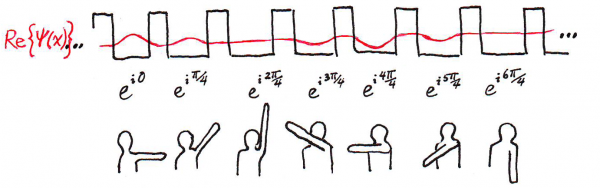
The red line in the figure above represents the real part of a LCAO wavestate at an instant in time. This is a single electron wavestate that is spread over many potential wells. Student volunteers will keep track of the time dependent coefficients (complex numbers) that multiply each atomic orbital in the LCAO.
Ask for nine volunteers to be “coefficients in a quantum wavestate, even more fun than being atoms in a crystal!” and have them stand at the front of the room (about two feet in front of the black board and one arm's width apart from one-another).
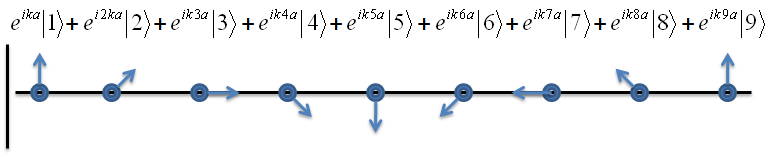
Draw a potential well behind each student. Establish that there is an atomic orbital associated with each well. Denote the atomic orbitals |1>, |2>, |3> etc. Each atomic orbital will play a role in the LCAO state. Denote the repeat distance of the system, a. Establish a sign language for complex numbers: Your left arm points straight out representing exp(iφ) on a complex plane.
On the board, write the equation: SUM OVER j {(exp(i*2πx/8a - ωt)|j>}. Ask the students to act it out this LCAO.
On the boards, write the equation: SUM OVER j {(exp(i*2πx/4a - ωt)|j>}. Ask the students to act it out this LCAO.
Activity: Student Conversations
What determines the value of ω in the LCAO.
Do you expect ω to be the same for both states that were acted out?
What happens if we super impose a left moving LCAO and a right moving LCAO with the same wavelength?