- §1. Harmonic Integrals
- §2. Completeness
- §3. Finding Coefficients
- §4. Example
- §5. The Gibbs Phenomenon
- §6. Symmetries
Harmonic Integrals
What happens if you multiply two different trig functions? For instance, consider the function $\sin(2\theta)\sin(3\theta)$, which is shown in Figure 1. It looks about as you might expect, with the overall structure of a trig function that “wiggles”. What is the area under this graph, that is, what is its integral? Hard to tell, but there's about as much above the axis as below, so zero would be plausible guess, which turns out to be correct. This idea underlies all of Fourier theory.
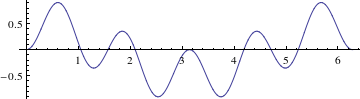
Figure 1: The graph of $y=\sin(2\theta)\sin(3\theta)$.
It is in fact not that difficult to evaluate such integrals in closed form, for instance, \begin{align} \int \cos(m\theta) \cos(n\theta) \,d\theta &= \frac{m\,\sin(m\theta)\cos(n\theta)-n\,\cos(m\theta)\sin(n\theta)} {m^2-n^2} \end{align} for $m\ne n$. In the above example $m$ and $n$ are both integers, and we are looking at an entire period; with these assumptions, we have \begin{align} \int_0^{2\pi} \sin(m\theta) \sin(n\theta) \,d\theta &= 0 ,\label{sinsin}\\ \int_0^{2\pi} \sin(m\theta) \cos(n\theta) \,d\theta &= 0 ,\\ \int_0^{2\pi} \cos(m\theta) \cos(n\theta) \,d\theta &= 0 . \label{coscos} \end{align} Of course, if $m=n\ne0$ is an integer, we have a different result, namely \begin{align} \int_0^{2\pi} \sin^2(m\theta) \,d\theta &= \pi ,\\ \int_0^{2\pi} \sin(m\theta) \cos(m\theta) \,d\theta &= 0 ,\\ \int_0^{2\pi} \cos^2(m\theta) \,d\theta &= \pi . \label{cos2} \end{align}
To complete this list, we consider the case $m=0$. Since $\sin(0\,\theta)=0$, it is enough to examine $\cos(0\,\theta)=1$. But (\ref{sinsin})–(\ref{coscos}) hold even for $m=0\ne n$, although (\ref{cos2}) must be replaced by \begin{equation} \int_0^{2\pi} \cos^2(0\,\theta) \,d\theta = 2\pi . \end{equation}
 Move content about inner products from this section to this section.
Move content about inner products from this section to this section.